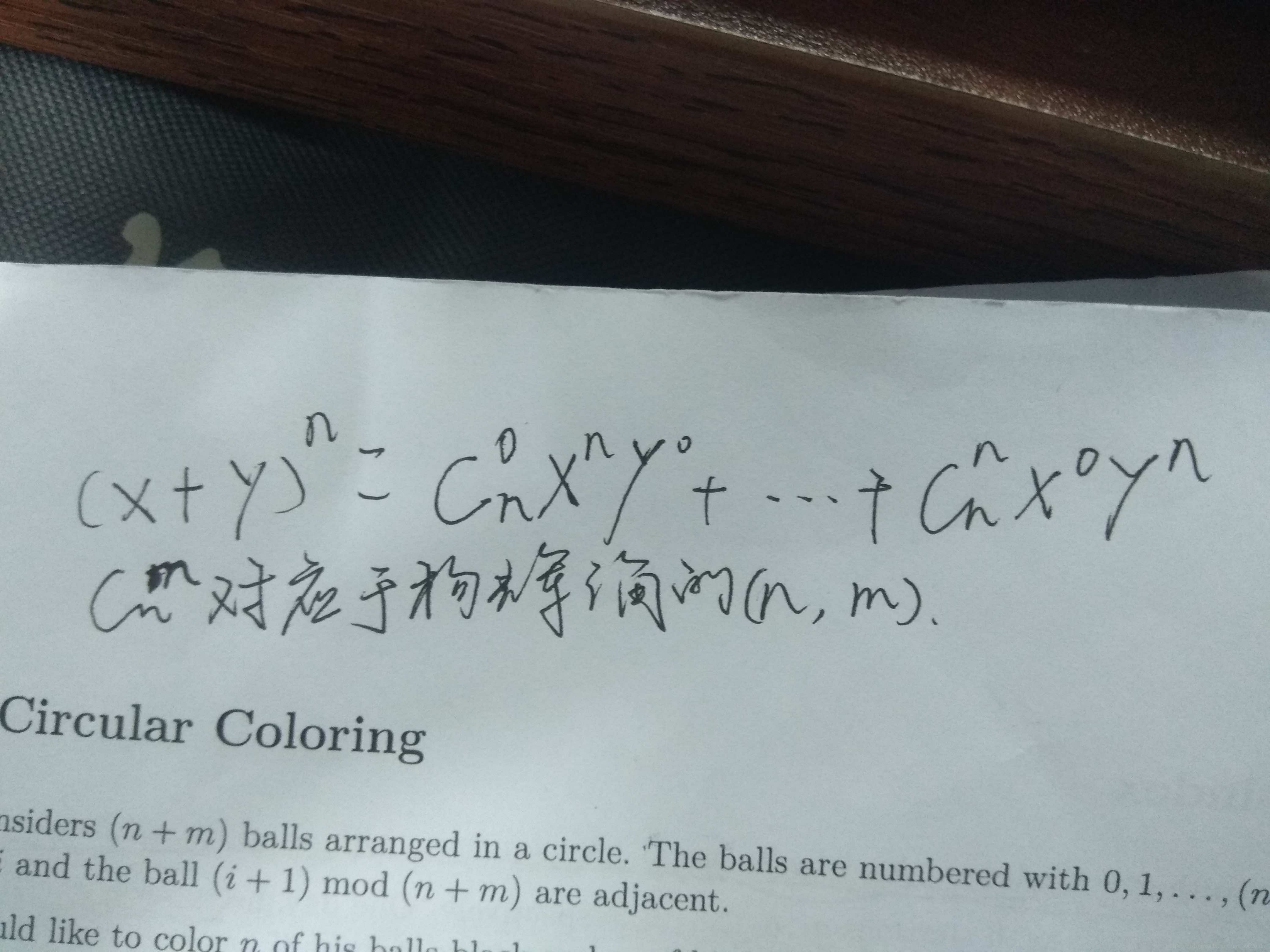杨辉三角
警告
本文最后更新于 2021-09-26,文中内容可能已过时。
百度知道 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1、每行数字左右对称,由 1 开始逐渐变大,然后变小,回到 1。 2、第 n 行的数字个数为 n 个。 3、第 n 行数字和为 2^(n-1)。 4、每个数字等于上一行的左右两个数字之和。可用此性质写出整个帕斯卡三角形。 5、将第 2n+1 行第 1 个数,跟第 2n+2 行第 3 个数、第 2n+3 行第 5 个数……连成一线,这些数的和是第 2n 个斐波那契数。将第 2n 行第 2 个数,跟第 2n+1 行第 4 个数、第 2n+2 行第 6 个数……这些数之和是第 2n-1 个斐波那契数。 6、第 n 行的第 1 个数为 1,第二个数为 1×(n-1),第三个数为 1×(n-1)×(n-2)/2,第四个数为 1×(n-1)×(n-2)/2×(n-3)/3…依此类推。
此数列中各行中的数字正好是二项式 a+b 乘方后,展开始终各项的系数。如:
| |
相关内容
Buy me a coffee~
 支付宝
支付宝 微信
微信